|
|
|
|
|
|
Impedance Matching. Part 3: L-Network Solutions.
By David Knight G3YNH
Contents:
|
<<< Part 2 . 1. L-networks, overview. 2. Network solutions for XpXs. 3. Network solutions for XsXp. 4. L and C range calculations. 5. Lossy networks. |
6. Lossy XpXs networks. 7. XpXs network efficiency. 8. Lossy XsXp networks. 9. XsXp network efficiency. 10. Efficiency calculations. Part 4 >>> . |
|
1. L-networks: The antenna (or arbitrary load) impedance matching problem can be solved (at least in principle) using only L-networks. Such networks naturally give rise to solutions that avoid excessive excursions in the Z-plane; which means that they are likely to be efficient in terms of power transfer. The L-network approach also involves only two variables for two unknowns. This means that it can be implemented in simple algorithms that are guaranteed to terminate; the termination criterion being obtained by using null-indicators for resistance, conductance and phase (or reactance) [see 6.5]. Prior to the development of the R, G, φ method (Underhill & Lewis, 1973 [9] ), automatic matching systems offering guaranteed termination used impedance-magnitude and phase as the solution criteria. In that case, the magnitude null measurement was used directly for the adjustment of a variable impedance transformer (see for example: Collins 180L-3); but the downside is that efficient continuously-variable wideband RF transformers are difficult to realise. L-networks, on the other hand, use reactive voltage or current magnification for the transformation; which means that the efficiency issue, although ever present, centres on the more tractable problem of how to design good variable inductors and capacitors. There are eight possible reactive L-networks, which are shown below in relation to some of the Z-plane operations for which they can be used: |
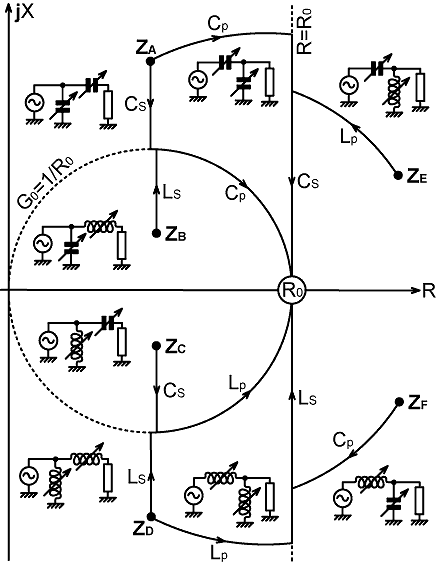
| The diagram suggests a nomenclature for discussing these networks. Take, for example the impedance ZA, which has a resistive component that is less than R0 (the target resistance, usually 50Ω), but lies outside the G0 constant conductance circle (i.e., G<1/R0). There are two ways in which this impedance can be transformed to R0 using a pair of variable capacitors (an LC solution is also possible, but we will leave discussion of that until later). A capacitor in series can be used to shift the impedance onto the G0 circle. A capacitor in parallel with that combination will then move the impedance around the G0 circle to R0. We might designate this operation (and the network that performs it): CsCp. Alternatively, a capacitor in parallel parallel with ZA will shift it onto the R0 constant-resistance line. A capacitor in series with the combination will then move the impedance down the line to R0. This latter operation can be designated CpCs. Thus we can define the eight networks of interest: |
| L-network | Circuit configuration |
|
|
Capacitor in series with load, capacitor in parallel with generator. |
|
|
Capacitor in parallel with load, capacitor in series with generator. |
|
|
Inductor in series with load, capacitor in parallel with generator. |
|
|
Capacitor in series with load, inductor in parallel with generator. |
|
|
Inductor in series with load, inductor in parallel with generator. |
|
|
Inductor in parallel with load, inductor in series with generator. |
|
|
Inductor in parallel with load, capacitor in series with generator. |
|
|
Capacitor in parallel with load, inductor in series with generator. |
| One slightly annoying feature of this notation is that is in contradiction to the habit of drawing circuit diagrams in such a way that electrical power flows from left to right. There is however, no rule saying that circuit diagrams have to be drawn in that way, and it is by no means a universal convention. The transformation of an arbitrary impedance to a target resistance however is a set of logical operations, and the nomenclature captures the sequence. To illustrate the point, consider the effect of the CpLs network on the impedance ZF: |
|
ZF |
→ |
R=R0 |
→ |
Z=R0+j0 |
|
Thus the order reflects the operations performed on the randomly-encountered
impedance in order to achieve the target resistance. An observation that we will now make regarding the eight networks is that there is considerable redundancy in the set. On the diagram above, the impedances ZA and ZD are both shown as having two ways in which they can be brought to R0, and even those solutions are not unique. Furthermore we may note the practical wastefulness of the situation. If we have two variable inductors, two variable capacitors, and some switches, we can make any one of the eight networks as required; but there will always be two components that are not used. Allowing all eight possibilities effectively doubles the cost and weight of the matching network. It is, of course, not strictly admissible to introduce practical issues into the basic logical considerations; but such pragmatism can be justified in this case. The point is that; if we reduce the set of networks to include only those that involve a single inductor and a single capacitor, it is still possible to find solutions for all parts of the Z-plane. That restriction is applied in the diagram below: |
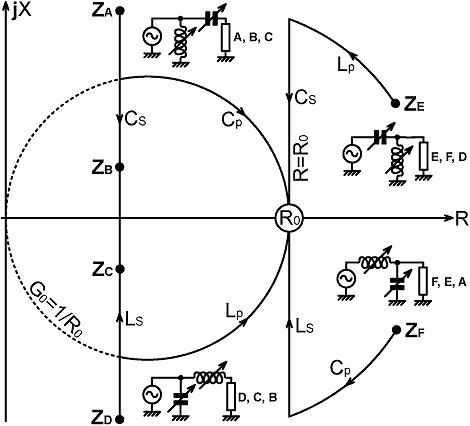
|
There is considerable redundancy even now, and we can certainly
still find solutions for any starting impedance. Firstly, notice
that both the CsLp
and the LsCp networks
can match impedances (ZB and ZC) that fall inside the G0
circle (i.e., when G>G0). Also, although
the LpCs network
gives a short route for matching ZE,
it can perfectly well be used to shift impedances ZD
and ZF around long arcs until they
meet the R0 constant resistance line at
a point having positive reactance. Likewise, the CpLs network can shift impedances ZA
and ZE until they meet the R0 line with negative reactance. The long-arc
solutions might not be optimal in terms of efficiency, but they
will increase the possible matching range in the (somewhat likely)
event that infinitely variable capacitors and inductors should
prove to be unavailable. These considerations, incidentally, show why the traditional π and T networks can both (in principle) match any impedance with one of the controls set for minimum effect. The CsLp and LpCs networks can be regarded as CLC-T networks with one of the capacitors set to a very large value. Similarly, the CpLs and LsCp networks can be regarded as CLC-π networks with one of the capacitors set to a very small value. Either choice offers solutions for every part of the Z-plane, as shown in the table below: |
|
|
|
Z-plane regions |
|
|
|
A, B, C |
|
|
D, E, F | |
|
|
|
A, E, F |
|
|
B, C, D |
|
The advantage of using a π or T network is that three-component
solutions are sometimes possible when limitations of the adjustment
range prevent two component solutions. Also, no switching is
required. The disadvantages however are that these networks sometimes
force long-arc solutions, three-parameter solutions cannot be
determined analytically, and one of the capacitors is redundant.
By including switches to allow any one of the four LC L-network configurations, a variable capacitor is eliminated, the fundamental necessity for long-arc solutions is removed, and the matching range that can be achieved without the need for three-parameter solutions is increased. The only apparent downside, is that some of the solutions for starting impedances having a resistive component of less than R0 involve crossing the zero reactance axis. Observe, for example. that when matching ZD using an LsCp network, it is necessary to meet the G0 circle on the positive reactance side. The objection must be put into perspective however. In practical antenna matching situations involving low input resistance (e.g., electrically-short antennas), it is normal to encounter reactance magnitudes of many hundreds (and sometimes thousands) of Ohms. For a 50Ω target resistance however, the maximum distance across the G0 circle is 50Ω. Hence the extra reactance needed to cross the circle will usually be small in comparison to the total, and so the extra loss resistance will be relatively small. A suitable switching arrangement is shown below. Also shown is the set of diagnostics that will enable the switch settings to be determined, the actual bridges being described in [6.5]. Also recommended when feeding a balanced antenna system is the practice of placing the balun transformer at the constant-impedance side of the matching network, the point being to minimise losses by using a transmission-line transformer with a characteristic resistance equal to R0. This requires, of course, that the network be built on a floating chassis with electrically insulating control and actuator rods. |
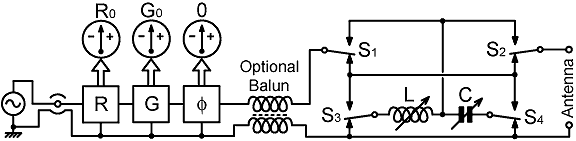
| The switchable network on the right can be referred to as the "short-path" AMU, because it allows matching to occur with short, although not necessarily minimal, excursions in the Z-plane. The truth table for the switches (assuming relays de-energised as per the diagram) is shown below: |
|
|
|
|
|
|
Application: |
|
|
|
|
|
|
Load evaluation. Matching Z = R0 |
|
|
|
|
|
Antenna disconnect | |
|
|
|
|
|
Transceiver disconnect | |
|
|
|
|
|
|
Parallel reactance, variable near zero |
|
|
|
|
|
|
LC series network in parallel. |
|
|
|
|
|
|
Matching Z-plane regions D, C, B |
|
|
|
|
|
|
Matching Z-plane regions F, E, A |
|
|
|
|
|
|
Matching Z = R0 // jXL (when G=G0) |
|
|
|
|
|
|
LC series network in parallel. |
|
|
|
|
|
|
Matching Z-plane regions A, B, C |
|
|
|
|
|
|
Matching Z-plane regions E, F, D |
|
|
|
|
|
|
Matching Z = R0 // jXC (when G=G0) |
|
|
|
|
|
|
|
|
|
|
|
|
|
Conjugate reactance, variable near zero |
|
|
|
|
|
|
Conjugate reactance, variable near zero |
|
|
|
|
|
|
| Notice that out of the sixteen possible system states, some are redundant, some are not particularly useful, and the ones that place an LC series network across the transmission line are probably best avoided. Now, if we discard everything except those states associated with L-networks, a simple pattern emerges: |
|
|
|
|
|
|
Application: |
|
|
|
|
|
|
Load evaluation. Matching Z = R0 |
|
|
|
|
|
|
Matching Z-plane regions D, B, C |
|
|
|
|
|
|
Matching Z-plane regions F, E, A |
|
|
|
|
|
|
Matching Z-plane regions A, C, B |
|
|
|
|
|
|
Matching Z-plane regions E, F, D |
| If the component adjustment ranges are sufficient to allow matching via the shortest available route through the Z-plane, then the decision to operate either S2 or S1 can be based entirely on whether the resistive component of the impedance to be matched is >R0 (regions E, F), or <R0 (regions A, B, C, D). What we need to determine now is whether that ideal situation can be realised in practice, and whether or not longer routes might sometimes lead to greater efficiency than short ones. There might, for example, be situations in which a long arc solution involving a parallel capacitor is better than a shorter arc achieved using an inductor; for the simple reason that practical inductors are always more lossy than capacitors. |
|
2. Network solutions
for XpXs. The best approach to determining the component values required for a matching solution is to obtain analytical expressions for L and C in terms of the starting impedance. This, as we will now see, is straightforward, but algebraically rather messy. The required derivations have two saving graces however: firstly that the correct solutions will be obvious from the qualitative picture of Z-plane operations developed in the preceding sections; and secondly that, from a theoretical point of view, there are only two reactive L-networks. We can either put one reactance in parallel with the load and one in series with the generator (XpXs) or vice versa (XsXp). In this section, we will analyse the XpXs network. |
| The solution state for the XpXs network is illustrated on the right. An arbitrary load Z=R+jX is presented, and the reactances Xp and Xs are chosen so that the impedance looking into the network is the target load resistance R0. To find the solutions (there will be more than one), we begin by writing the expression for R0 in terms of the circuit parameters; i.e.: |
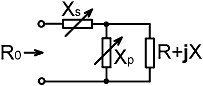 |
|
R0 = jXs
+ [ jXp // (R+jX) ] Expanding the parallel product gives: |
|
|
R + j(X + Xp) |
| Multiplying the numerator and denominator of the second term by the complex conjugate of its denominator gives: |
|
|
R² + (X + Xp)² |
| Which can be expanded thus: |
|
|
R² + (X + Xp)² |
|
|
R² + (X + Xp)² |
| Now observe that R0 is purely real. Therefore the real part of this expression is R0 and the imaginary part is zero. Hence we obtain a pair of simultaneous equations: |
|
|
These equations must now be solved; but they also remain important
in their own right because they can later be used to test the
results of calculations to ensure that the solutions and subsequent
spreadsheet or program codings are correct. Now, bearing in mind that R0, R and X are input parameters, and the solution variables are Xp and Xs; we can see straight away that a value for Xs is obtained from equation (2.2) on providing a value for Xp. Also Xp is the only variable appearing in equation (2.1), and so no cross substitutions are required in finding the solutions. Rearranging (2.1) gives: R0 [ R² + (X + Xp)² ] - RXp² = 0 R0 [ R² + X² + Xp² + 2XXp] - RXp² = 0 R0R² + R0X² + R0Xp² + 2R0XXp - RXp² = 0 Hence: (R0 - R)Xp² + 2R0XXp + R0(R² + X²) = 0 . . . . (2.3) This is a quadratic equation in Xp with a=(R0-R) , b=2R0X and c= R0(R² + X²). Real solutions will exist when: b²-4ac = (2R0X)² - 4(R0 - R)R0(R² + X²) ≥ 0 Multiplying out: b²-4ac = 4[ R0²X² - (R0² - R0R)(R² + X²) ] = 4[R0²X² - R0²R² + R0R³ - R0²X² - R0RX²] Hence: b²-4ac = 4R0R(R² + X² - R0R) Since both R0 and R must be finite in order for power transfer to occur, the sum of the terms in the bracket must be ≥0 if real solutions are to exist. Hence, impedance matching is possible when: R² + X² ≥ R0R This means that the XpXs network can provide solutions for impedances that lie outside an area in the Z-plane bounded by the expression: R² + X² - R0R = 0 . . . . (2.4) This is the equation of a circle [see 5.1-5] and can therefore be characterised by comparing it with the general circle equation, which can be written in the Z-plane co-ordinate system: R² + X² -2RRc -2XXc + Rc² + Xc² - r² = 0 where r is the radius, and Rc and Xc are the co-ordinates of the centre point. Equation (2.4) has no terms equivalent to -2XXc, and so Xc is zero. The centre lies on the R axis. This reduces the circle equation to: R² + X² -2RRc + Rc² - r² = 0 Equation (2.4) has no terms equivalent to Rc²-r², therefore these two terms cancel and (neglecting negative resistance solutions) Rc=r. This means that the circle passes through zero at its extreme left-hand point in the Z-plane. The circle equation is now reduced to: R² + X² -2RRc = 0 Thus we identify R0 = 2Rc The centre of the circle lies at R0/2, and since Rc=r, the circle also has a radius of R0/2. This circle is, of course, the G0 constant-conductance circle, and the algebra is telling us that the XpXs network can provide matching solutions for any impedance that lies on or outside it. Hence, as we already knew from geometric considerations, the general solution criterion for XpXs networks (i.e., CpLs and LpCs) is G ≤ G0. Now, to solve equation (2.3) for Xp, we use the standard formula for quadratic equations, inserting a, b and c as defined above. The result is: |
|
|
2(R0 - R) |
| This, presuming that the criterion for real solutions is met, is a two-valued function; as must be expected because we know that there are options regarding the choice of network for matching impedances outside the G0 circle. The separate solutions are: |
|
|
Notice that the denominator in either case becomes negative when
R>R0. Hence both of these expressions
can be either positive or negative, and so both can correspond
to solutions involving either an inductor or a capacitor. Also
notice that when R=R0, the required parallel
reactance goes to infinity. This is as we expect, since all that
is required to match an impedance Z=R0+jX
is a series conjugate reactance. Now, to find a convenient expression for Xs, we start by rearranging equation (2.2): |
|
|
R² + (X + Xp)² |
|
Equation (2.1) however shares
the same denominator and so can be rearranged to provide the
substitution: R² + (X + Xp)² = RXp² / R0 Hence: |
|
|
RXp² |
i.e.:
This function is also two-valued because the input value for Xp can come from either (2.5a) or (2.5b). Also, if we put R=R0, then: Xs = -[ R² + X² + XXp ] / Xp but when that happens, Xp→∞. Hence, only the XXp term can survive being divided by Xp, and so Xs→ -X. |
|
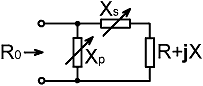
3. Network solutions
for XsXp. The XsXp network solutions can be found using an approach similar to that used in the previous section (although the algebra comes out somewhat differently). Referring to the diagram on the right, the required information is embedded in the expression: R0 = jXp // [ R + j(X + Xs) ] Expanding the parallel product gives: |
 |
|
|
R + j(X + Xs + Xp) |
|
R + j(X + Xs + Xp) |
| Multiply numerator and denominator by the complex conjugate of the denominator, then expand, cancel opposing terms, and regroup: |
|
|
R² + (X + Xs + Xp)² |
|
|
R² + (X+Xs+Xp)² |
|
|
R² + (X+Xs+Xp)² |
| As before, the real part of this expression is R0 and the imaginary part is zero. Thus we obtain the two simultaneous equations: |
|
|
As before, these equations can be used for checking the subsequent
solutions and calculations. Now notice, in equation (3.2), that Xp cannot be zero (a short-circuit across the generator) if power transfer is to occur. Therefore the terms in square brackets in the numerator must add-up to zero; i.e.: R² + (X+Xs)(X+Xs+Xp) = 0 This can be rearranged to obtain an expression for Xp in terms of Xs: R² + (X+Xs)² + Xp(X+Xs) = 0 i.e.:
Rearranging (3.1) gives: R0[ R² + (X+Xs+Xp)² ] = RXp² and substituting for Xp using (3.3): R0{ R² + [X + Xs - X - Xs - R²/(X+Xs) ]² } = R[ -(X+Xs) -R²/(X+Xs) ]² R0[ R² + R4/(X+Xs)² ] = R[ 2R² + (X+Xs)² + R4/(X+Xs)² ] R0R + R0R³/(X+Xs)² = 2R² + (X+Xs)² + R4/(X+Xs)² Multiply throughout by (X+Xs)² : R0R(X+Xs)² + R0R³ = 2R²(X+Xs)² + (X+Xs)4 + R4 i.e.: (X+Xs)4 +(2R²-R0R)(X+Xs)² +(R4-R0R³) = 0 This, although it looks horrible, is merely a quadratic equation in (X+Xs)² , with a=1, b=(2R²-R0R) and c=(R4-R0R³). In this case: b²-4ac = (2R²-R0R)² - 4(R4-R0R³) = 4R4 + R0²R² - 4R0R³ - 4R4 + 4R0R³ hence: √(b²-4ac) = ±R0R which, since neither R0 nor R will be negative in practice, means that the solution for (X+Xs)² is real. Thus: (X+Xs)² = [-(2R²-R0R) ±R0R]/2 We expect an exclusion (i.e., imaginary solutions) for some parts of the Z-plane nevertheless; and this comes from taking the square root: Xs = -X ±√[ (R0R ±R0R -2R²)/2 ] The negative possibility for the middle term in the square-root bracket always results in an imaginary solution, and so can be excluded. Hence: Xs = -X ±√[ R(R0-R) ] . . . . . . (3.4) This expression will only give real solutions when R ≤ R0. The restriction is, of course, exactly as expected from the discussion earlier in which it was established that the XsXp type networks can only be used for matching loads that fall in regions A, B, C or D of the Z-plane. Notice also that when R=R0, Xs=-X, and if we substitute that condition into (3.3) we will find that Xp→∞. When R=R0, any parallel reactance must be open-circuit, and matching is accomplished using only a series conjugate reactance. The two possible solutions for Xs are thus: Xs = -X +√[ R(R0-R) ] OR Xs = -X -√[ R(R0-R) ] The calculated result from either expression can be put into (3.3) in order to obtain a value for Xp, but the problem can be made more computationally efficient by defining an intermediate variable, thus: U = +√[ R(R0-R) ] Hence: Xs = -X ±U substituting this into (3.3) gives: Xp = -[X -X ±U + R²/(X -X ±U) ] This is a two-valued expression for Xp, but notice that the solutions are strictly paired with the corresponding solution for Xs ; i.e., we must use either +U or -U to determine both reactances, the choice is not arbitrary. Thus overall: |
|
Xs = -X +U AND Xp = -U -R²/U OR Xs = -X -U AND Xp = +U +R²/U |
Where U = +√[ R(R0-R) ] and provided that: R ≤ R0 |
3.5b |
|
4. L and C range calculations: The calculation of network L and C values is most easily illustrated by an example; which is given in the open-document spreadsheet file: smallgarden.ods . For this, the input impedance of a fairly typical small HF antenna (30 m of wire, 9 m above the ground, centre fed with 10 m of 600 Ω line) was simulated from 1.6 MHz to 30 MHz using EZNEC+. The antenna is defined in the file: smallgarden.EZ. The impedance data, provided by EZNEC as a comma-separated variable (CSV) list, were then imported into into a spreadsheet file (using the file/open dialogue) and all extraneous data except for f, R and X were deleted. The following calculations and logical operations were then performed: Z-plane region: To determine the Z-plane region, first calculate the antenna input conductance: G = R/(R²+X²) The logic is then: R<R0 , G<1/R0 , X>0 → A R<R0 , G>1/R0 , X>0 → B R<R0 , G>1/R0 , X<0 → C R<R0 , G<1/R0 , X<0 → D R>R0 , G<1/R0 , X>0 → E R>R0 , G<1/R0 , X<0 → F XpXs solutions are not possible for regions B and C. XsXp solutions are not possible for regions E and F. XpXs calculations: These are performed using formulae (2.5) and (2.6), and the reactances obtained are fed back into equations (2.1) and (2.2) to check the coding (the check columns are hidden to reduce clutter). Each reactance is turned into a capacitance using: C = -1/(2πfX) and into an inductance using: L = X / (2πf) When the capacitance is positive, the required reactance can be provided by a capacitor. When the inductance is positive, the required reactance can be provided by an inductor operating below its parallel self-resonance frequency (SRF). The graphs are provided with movable limit bars. Vacuum capacitors have an adjustment range of about 100:1. Air capacitors usually have an adjustment range between about 25:1 and 10:1. A large variable inductor might have a range from about 0.1 to 60 microHenries at low short-wave frequencies (not counting the inductance of the connecting wires). At frequencies above the point at which the inductor exhibits parallel self-resonance at its maximum setting, the effective maximum available inductance is infinite. An inductor has negative reactance when operated just above its SRF (it turns into a capacitor), but this property is too specific to the device and the circuit layout to be considered in a general model. XsXp calculations: These calculations use formula (3.5) and are checked by feeding the reactances into equations (3.1) and (3.2). The Xp calculation is also checked using equation (3.3). The component value and range determination procedure is as for the preceding case. Transmitter-side balun: The value for R0 on each worksheet is obtained from a single cell. This is done so that the effect of placing a step-up or step-down balun transformer between the transmitter and the matching network can be determined by changing R0. If the target value is 50 Ω for a 1:1 balun: then the effect of a 4:1 impedance transformer (2:1 turns ratio) can be simulated by changing R0 to 12.5 Ω; and the effect of a 1:4 transformer can be simulated by changing R0 to 200 Ω ; etc. Findings: For the example antenna, a 10 pF to 1000 pF capacitor and a 0.1μH to 60 μH inductor can match any of the impedances presented between 1.6 MHz and 30 MHz using a 1:1 balun; and at frequencies above 3.5 MHz, there are always two possible LC L-network solutions. The example antenna was deliberately chosen to be awkward at lower frequencies (where it is electrically short) and matching networks often cannot cope in such circumstances. Spreadsheet template: The example spreadsheet can, of course, be used as a template for investigating the matching of any antenna or spot impedance. It is simply a matter of pasting (f, R, X) data into the first three columns. |
|
5. Lossy Networks: The networks considered in the preceding sections are, of course, ideal. Resistive losses will affect the matching solutions, but not sufficiently to invalidate adjustment-range calculations; unless poor quality components are used; or unless severe eddy-current losses and inductance cancellation are incurred by building the network inside a small case made from a material of poor RF conductivity (such as steel). Note however that parallel losses (in particular) tend to make antenna matching easier, rather than more difficult, because they combine with the load impedance and thereby reduce the extremes of impedance magnitude that are likely to be encountered. The primary focus of interest when considering losses is the calculation of network efficiency. Before we go on to put component resistances into the models however, it is necessary to establish an important caveat. It is not unusual to come across articles that naively assume that variable inductors have approximately constant Q. This is simply not true. Admittedly, the Q at a particular inductance setting will change fairly slowly with frequency; but overall the Q depends on the length of wire used, the solenoid length/diameter ratio at the required setting, the self-capacitance, and the eddy-current losses in any shorted-turns or shielding box. Hence the ability to include spot Q or resistance values, while interesting if used judiciously, does not solve the general efficiency-estimation problem. The general problem is, in fact, not analytical. The reason is that, for a particular load impedance, we must first find a matching solution before we can determine the component settings, and the component settings must be established before we can determine the losses. The losses must then be fed back into the model, thereby changing the settings (hopefully by only a small amount), and a new solution must be obtained. Hence, efficiency calculation is an iterative process; and its full solution requires, for the inductor in particular, either a large table of Q vs. frequency measurements for every turn or so of the control-shaft, or a comprehensive mathematical model. Hence the remit of the following sections is only to show how to put loss resistances into the models. How to determine the values of those resistances is a separate matter. Mercifully however, capacitor losses can usually be neglected; especially if vacuum capacitors are used, in which case the ESR (equivalent series resistance) is usually less than the AC resistance of the connecting wires. We cannot simplify the mathematics by neglecting capacitor losses at the outset however; for the simple reason that we don't know whether a network component will be a capacitor or an inductor until we determine the sign of the corresponding reactance. |
|
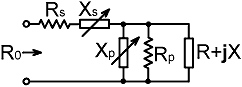
6. Lossy XpXs networks: An impedance can be represented either in series or parallel form. Hence a lossy network component can be represented either as a small resistance in series with a reactance, or as a large resistance in parallel with a reactance. In general, the reactance of the series form is not the same as that of the parallel form; but conversion between the two is a straightforward matter; and if the power loss is relatively small, then the difference is of little consequence when a reactance is converted into an inductance or capacitance value. Hence we are at liberty to choose whichever representation is the most convenient; and as we will see, it is best to use the series form for series components, and the parallel form for parallel components. |
| A lossy XpXs network is shown on the right; where Rs represents the losses in the series element Xs, and Rp represents the losses in the parallel element Xp. The forms so chosen allow us to lump Rs with R0, and Rp with the load impedance; which means that we can obtain solutions for Xs and Xp using the formulae given in section 2. |
 |
|
We start by lumping Rp
with the load impedance to obtain a new 'effective' load impedance: Z' = R' + jX' = Rp//(R+jX) Expand the parallel product, multiply numerator and denominator by the complex conjugate of the denominator, rearrange and cancel opposing terms: |
|
|
Rp+R + jX |
|
(R+Rp)² + X² |
|
|
(Rp+R)² + X² |
|
|
(Rp+R)² + X² |
|
The effective input impedance for the purpose of finding network
solutions is that which gives R0 when
Rs is added to it; i.e.:
The network solutions are now given by adding primes to the parameters of equations (2.5) and (2.6). |
|
|
Thus the existing solutions can be re-used by writing a pre-calculation
routine that takes in the raw data (R, X, R0)
and gives out (R', X', R0'). Notice here,
that in determining whether a solution is possible, the Z-plane
region must be decided using the processed data, not the raw
data. Hence, the conductance that establishes the operative region
is: G' = R'/(R'²+X'²) |
|
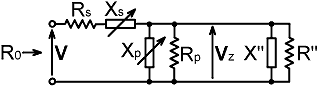
7. XpXs Network efficiency: Assuming that the difficulties involved in modelling the RF resistances of the components can be surmounted; the efficiency of a matching network is given by the ratio of the power delivered to the load against the power delivered by the generator; i.e., η = Pout / Pin Where η (Greek "eta") is the 'efficiency factor' (i.e., a number between 0 and 1); which can be converted into a percentage by multiplying it by 100, or into a figure in dB using: Network loss / dB = -10Log10(Pout / Pin) = 10Log10(Pin / Pout) Power can be calculated as the square of a voltage magnitude divided by a resistance. This is straightforward in the case of the power supplied by the generator, because the efficiency is determined on the basis that an impedance-matching solution has been found. Thus, if the voltage at the generator terminals is V: Pin = |V|² / R0 This leaves us with the problem of how to determine the output power using V, the point being to make the voltages cancel when we take the ratio, so that we are left with an expression involving only circuit parameters. For the XpXs network, we start by defining the voltage across the load as VZ and converting the load impedance into its parallel form: Z = R + jX = R" // jX" Where, using the series-parallel transformations [AC Theory, Section 19] we have: |
|
R" = (R² + X²) / R = 1/G and X" = (R² + X²) / X Thus: Pout = |VZ|² / R" which gives: |
 |
|
Pin |
|
|V|² R" |
|
|V|² (R² + X²) |
(7.1) |
|
The voltage magnitude ratio can be obtained from the voltage
ratio (see [AC
Theory, Section 24] ) thus: |VZ| / |V| = |VZ / V| and the voltage ratio, as can be seen from the diagram above, is a rather messy potential-divider problem: |
|
V |
|
Rs + jXs + ( R" // Rp // jX" // jXp ) |
|
Trying to expand this expression on paper is likely to exacerbate
global de-forestation, but we can just as well work with the
reciprocal by making use of the magnitude reciprocal theorem
[AC Theory,
24.2]: 1 / |VZ / V| = |V / VZ| where: |
|
VZ |
|
( R" // Rp // jX" // jXp ) |
|
( R" // Rp // jX" // jXp ) |
|
VZ |
|
|
R" |
|
Rp |
|
jX" |
|
jXp |
|
|
VZ |
|
R" |
|
Rp |
|
X" |
|
Xp |
+ j |
|
R" |
|
Rp |
|
X" |
|
Xp |
|
| This is now in the a+jb form, and so we can take the magnitude, i.e., √(a²+b²) ; but since we actually want the square of the magnitude, there is no need to take the square root. Thus we have: |
|
|
VZ |
|
2 |
|
|
|
R" |
|
Rp |
|
X" |
|
Xp |
|
2 |
+ |
|
R" |
|
Rp |
|
X" |
|
Xp |
|
2 |
(7.2) |
|
Where: R" = (R²+X²)
/ R and X"
= (R²+X²) / X and the network efficiency is given by: |
|
Pin |
|
R" |
|
|
VZ |
|
2 |
(7.3) |
|
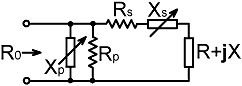
8. Lossy XsXp networks: Once again, we can re-use the existing network solutions by lumping the loss resistances with the other circuit parameters. In this case, a new effective load impedance is given by: Z' = R + Rs + jX |
|
and the effective load resistance is: R' = R + Rs When a matching solution has been found, the impedance looking into the network is R0, and so the effective target load resistance is that which gives R0 when placed in parallel with Rp; i.e.: R0' // Rp = R0 Taking the reciprocal and rearranging gives: |
 |
|
R0' |
|
R0 |
|
Rp |
|
R0 Rp |
|
Hence: R0' = R0 Rp / (Rp - R0) Notice here that R0' goes to infinity when Rp = R0, and we will need a negative value of R0' (power from both the generator and the antenna) to get a matching solution when Rp < R0. Practically, this means that we always want Rp >> R0, and that may not always be achievable in the event that a small value of inductive reactance is required for Xp. The Q of an inductance in parallel form is given by Rp/Xp, and it is by no means exceptional for a roller coil to have a Q in the region of 20 for low values of inductance. Hence solutions involving low positive values for Xp are likely to be associated with poor efficiency. A possible workaround is to alter the ratio of the balun transformer, so that R0 becomes very small; although there is a limitation here in that XsXp solutions are not possible when R' > R0'. Thus a likely effect of changing the balun ratio is to force an XpXs solution. The solutions for the lossy XsXp network are obtained by adding primes to R and R0 in the ideal-case formula (3.5), thus: |
|
Xs = -X +U AND Xp = -U -R'²/U OR Xs = -X -U AND Xp = +U +R'²/U |
Where U = +√[ R'(R0'-R') ] R' = R + Rs R0' = R0 Rp / (Rp - R0) and provided that: R' ≤ R0' |
8.1b |
| 9. XsXp Network efficiency: |
| In the XsXp case, the power output can be defined in relation to the hypothetical voltage VR across the resistive component of the load impedance. Obtaining the ratio of VR to the generator voltage V is a simple potential-divider problem: |
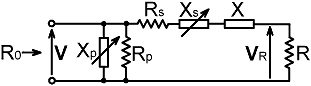 |
|
V |
|
R + Rs + j(X + Xs) |
|
(R + Rs)² + (X + Xs)² |
| The square of the voltage magnitude ratio is then: |
|
|
V |
|
2 |
|
[ (R + Rs)² + (X + Xs)² ]² |
|
(R + Rs)² + (X + Xs)² |
|
|
The output power is given by: Pout = |VR|²/R and the input power is given by: Pin = |V|²/R0 Taking the ratio, and substituting for |VR|²/|V|² using (9.1) gives the efficiency factor:: |
|
Pin |
|
(R + Rs)² + (X + Xs)² |
|
|
One initially perplexing feature of this expression is that it
does not appear to involve Rp. On examination
of (8.1) however, we see
that Xs is a function of R0',
and R0' is a function of Rp,
and so Rp will appear if a double substitution
is made. A full analytical verification is not necessary however.
When an XsXp network
calculation for the lossy case is set up, it will be found that
Pout/Pin →
1 when Rs is set to a very small value
and Rp is set to a very large value. A simple test of the limiting behaviour is nevertheless easily accomplished by setting Rs to zero in (9.2). In that case, assuming that Xs is also adjusted to the value required for infinite Rp, then Pout/Pin → 1 and we have: R² + (X + Xs)² = R0 R i.e.: (X + Xs)² = R0 R - R² which gives: Xs = -X ±√[ R(R0-R) ] This is identical to equation (3.4), and it is also the result obtained when R' is replaced with R and R0' is replaced with R0 in formula (8.1). |
|
10. Efficiency calculations: Once again, the network solution procedure is most easily illustrated by means of an example. Hence, in the spreadsheet file: lossy_L.ods , the calculation template used in section 4 has been extended using the formulae given in sections 6 to 9. As mentioned previously however, the calculation involves somewhat naive assumptions regarding component Q, and so the results need to be treated with caution. On examining the spreadsheet, it will be seen that columns have been added for the loss resistances Rp and Rs. In addition to being included in the overall calculation, these are used to calculate Q values for the reactance solutions using the expressions: Qp = |Rp / Xp| and Qs = |Xs / Rs| Putting Rp to a very large value (such as 1M Ω) and Rs to a very small value (such as 0.000001 Ω) causes the calculation to revert to the ideal case (i.e., efficiency → 1). Putting Rs to zero is not recommended, because it causes a divide-by-zero error in the Qs calculation. The Q values can be used as a guide for adjusting the loss resistances. The spreadsheet can also be made to adjust the loss resistance automatically to give a target Q by using the 'Goal Seek' tool. This is somewhat tedious, because it has to be done a cell at a time, and so only a few of the Qs have been adjusted to give meaningful efficiency estimates. The Q of a variable capacitor is typically 'somewhere around 1000'. In practice, this can mean anything from a few hundred to several thousand; but a little experimentation with the numbers will show that it tends to affect the efficiency factor only in the third or fourth decimal place. Hence the exact determination of capacitor Q is of little interest; and if the corresponding loss resistance is adjusted to give a Q of around 1000, a small improvement in realism is obtained for minimal effort. When the solution mandates a series capacitance however, we can reasonably say that the AC resistance of the capacitor arm will have a frequency dependence determined by the skin effect, which means that the ESR will be approximately proportional to √f. Hence, for the series capacitor solutions, the task of adjusting the Q has been eliminated in most instances by using the formula: Rs = 0.1√(f / MHz) i.e., it is assumed that the capacitor ESR (including the wiring) will be about 0.1 Ω at 1 MHz. This choice is fairly realistic, at least for those who wire up matching networks using copper or silver-plated strip. The important parameter in determining the efficiency is, of course, the coil resistance. This cannot be determined in the absence of a reference model for the variable inductor; and so the rough-and-ready approach, as used by typical 'ATU efficiency calculation' programs, is to make comparisons between different networks on the basis that the coil has a constant Q. In the example spreadsheet, the coil Q has been adjusted to 100 at various spot frequencies in order to test the conjecture (voiced throughout this chapter) that it is best to choose the matching solution that gives the shortest-path through the Z-plane. The results are shown in the table below; although it is important to understand that they do not constitute scientific proof. |
30m long centre-fed antenna + ladder line: AMU efficiencies based on coil Q = 100 [a]
|
/ MHz |
|
|
||||
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
[a] See spreadsheet file: lossy_L.ods
, [b] requires more than 1000 pF. [c] Capacitor Q adjusted to 1000 for comparison purposes. |
|
One issue that will be noted is that the AMU efficiency is low
when the antenna is electrically short. The lost power is also
dissipated almost entirely in the inductor. Before dismissing
the situation as hopeless however; it should be observed that
a good roller coil is perfectly capable of dissipating 50 W continuously,
and it takes only about 5 W of radiated power at the low end
of the HF spectrum to effect NVIS communications within a radius
of about 1000 km. With an AMU efficiency as low as 25%, a 100
W SSB transmitter will still deliver 25 W PEP to the antenna.
The peak matching-network loss in that case will be 75 W, but
the average loss will be about 25 W. Hence the coil will get
quite hot, but it is not likely to be damaged by a typical short-wave
transceiver. An interesting observation, which can be confirmed by experimenting with the numbers, is that extremely high efficiencies (>99%) are possible when the load impedance is such as to permit the use of dual capacitor L-networks. Such solutions are not relevent to the design of single-inductor, single-capacitor matching units, and only occur when the impedance lies in region A of the Z-plane; but they are viable in installations that work on a single frequency or over a very small range of frequencies. The point is that it might be possible to transform an impedance into region A, either by using a suitable length of transmission line, or by using a series loading coil. A loading coils is lossy, of course; but when mounted with the antenna (i.e., away from structures that cause eddy-current losses) it can have much greater Q than a roller inductor, and it can also contribute to the radiation field. |
© D W Knight 2009, 2013
David Knight asserts the right to be recognised as the author of this work.
|
|
|
|
|
|