|
|
|
|
|
|
Impedance Matching. Part 2: Popular Matching Networks.
By David Knight G3YNH and Nigel Williams G3GFC
Contents:
|
<<< Part 1 . 0. Introduction . 1. The π-network. 2. Fully variable π-match. 3. L-match. 4. Switched inductor π-match. 5. Tapped inductor with interpolation. 6. T-match. |
7. Reciprocal L-network. 8. Switched inductor T-match. 9. Differential T-match. 10. "Ultimate" Transmatch? 11. SPC Transmatch. 12. Discussion. Part 3 >>> . |
|
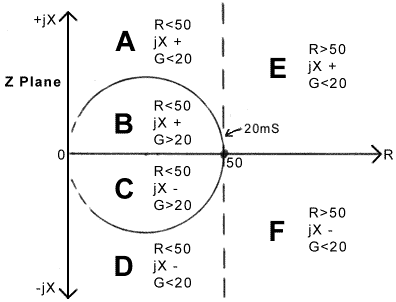
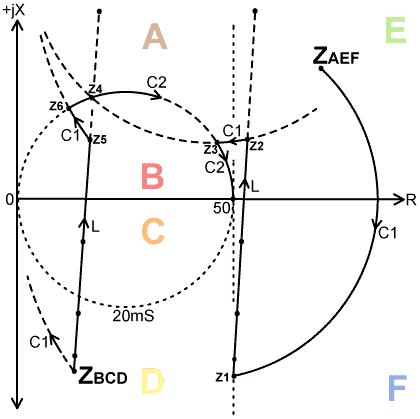
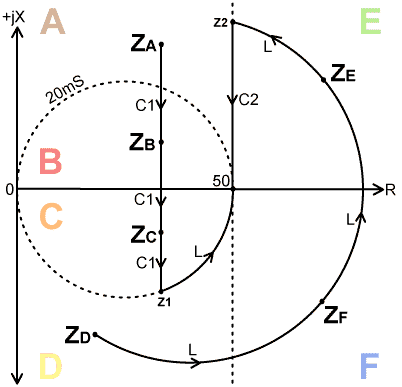
Introduction. In the following sections we show what happens in impedance space (i.e., in the Z-plane) when the various popular matching networks (antenna tuners) are adjusted. The adjustment operations are discussed on the basis that they can be monitored, in most cases, using a 'Match Meter', i.e., an RF bridge that gives null measurements of R, jX, and G. The insights gained by understanding what is happening in impedance space show how many of the common networks can be (simultaneously) simplified, made cheaper to build, made more foolproof, and made more efficient. The input impedance of an antenna system can be assigned (either notionally, or using a Match Meter or measuring bridge) to one of six regions of the Z-plane, as illustrated below. The assignment identifies the AMU adjustments that must be made in order to bring the impedance to 50+j0 Ohms using combinations of series and parallel reactance. Note that if the impedance lies on the boundary between two regions, it may be assigned to one or the other, or moved, depending on the matching network available. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Note also that if an AMU has in integral balun, it does not matter from the assignment point of view whether the balun is placed at the input side or the output side of the AMU. If a step-up or step-down balun is placed at the output (antenna) side, it will simply scale the antenna system impedance to give a new impedance, and it is this scaled impedance that must be matched. If a step-up or step-down balun is placed at the input (transmitter) side, it will scale all of the impedances seen by the monitoring bridge during the matching process, but it will also scale the target impedance, so making no difference to the operations involved. Consequently, any balun built into an AMU can be ignored for the purposes of analysing how the AMU works, but must be taken into account when determining the network component values. |
|
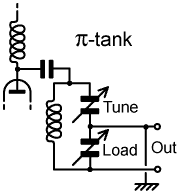
1. The π-network: Before examining the π-network, we must first make a distinction between the π-match and the π-tank, two devices that can have identical circuits but that nowadays perform very different functions. |
| The π-tank is the modern incarnation of the Collins Universal Coupler, which was advocated for direct matching of valve (electron-tube) anode circuitry to random antennas in the days before VHF communications. In current practice however, the universality has to be sacrificed in the interests of harmonic suppression, which means that the load impedance needs to be specified within fairly narrow limits. The π-tank in a valve RF amplifier should therefore be considered as a resonant transformer with a variable capacitive tap; which is normally intended to operate into a resistive load impedance of approximately 50Ω. When so designed, it usually has a fixed inductance for each band of operation, and because its matching range is limited, it can be made to double as a low-pass filter. |
 |
| A single-ended class AB valve amplifier, with a π-network coupler, can have a second harmonic component at its output terminals that is about 45dB weaker than the fundamental, provided that no attempt is made to use it to match a non-resonant antenna directly. The reason for caution is that the valve on its own can sometimes produce about 10% of second harmonic distortion, and so may produce a second harmonic output only 10dB weaker than the fundamental without the filtration offered by the resonant tank. Such an amplifier can, of course, be used to match co-ax fed antennas over a reasonably wide range of SWR; but random antennas, if they can be matched at all, may create situations in which the second harmonic signal is unattenuated, and it may even be possible to tune-up on the second harmonic. Consequently, when non-resonant, non-50Ω antennas are used, a valve amplifier should first be matched into a 50Ω resistor, and then connected to the antenna via an AMU. Further improvement of the harmonic attenuation is then obtained from the fact that the antenna is matched only at the fundamental frequency, and coupling of harmonic energy will be inefficient. |
| The π-match on the other hand is an AMU: It is not intentionally a resonant circuit on its own, but serves to provide a conjugate reactance and a resistance transformation in the process of matching a transmitter to an antenna system. Many articles have appeared in the amateur radio press over the years alluding, without proper analysis, to the superiority of the π-match over other types of AMU, on account of its similarity to a low-pass filter. The whole point of an AMU however, is to permit matching to a wide range of impedances, in which case, any low-pass filtering obtained is not controllable and, in some situations may be non-existent. This means that the signal fed into the π-match should already have been filtered to conform to legal requirements, and any further harmonic rejection obtained is incidental. Thus distanced from the problem of trying to make it perform two unrelated jobs requiring different component values; we will show how to set one up for maximum efficiency, and also how to set one up for minimum efficiency for those who may be interested in setting-fire to the inductor. |
|
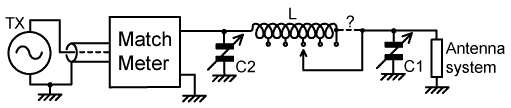
2. Fully variable π-match: The circuit configuration under consideration is shown below. In this, and subsequent examples, a 1:1 balun transformer can be inserted at any point in the signal chain (with suitable changes to the earthing arrangements) without affecting the matching process, and so baluns will be ommitted from the circuits shown. |
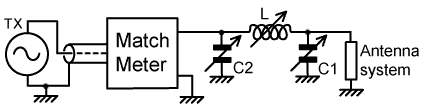
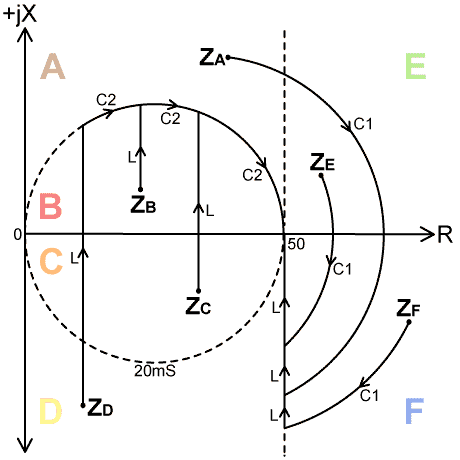
| When using a Match Meter, the first step is to examine the load impedance with the matching network components either disconnected or adjusted for minimum effect. In this case, the inductor L is set to minimum or shorted out, and the capacitors C1 and C2 are opened to minimum capacitance (maximum Xc) or disconnected (many commercial matching units also have a 'straight through' switch setting). Measurements of R, jX and G can then be used to assign the load to its Z-plane region, thereby identifying the adjustments required to match it to 50Ω. |
|
If the Load impedance lies in regions A, E, or
F, C1 is first increased to drive
the resultant impedance around a circle of constant conductance
until R=50Ω and jX is negative (as indicated by
the match meter). L is then increased to drive the impedance
along the 50Ω constant resistance line until jX=0,
at which point the impedance matching process is complete. Note
that adjustment of C2 is not required.
Note also that in some instances (e.g., load impedance in region
A) adjustment of C1 will initially cause
an increase in the resistance reading. For adjustment of C1 therefore, the match meter should first be
set to read jX and switched to read R as soon as jX
has become slightly negative. The meter should then be switched
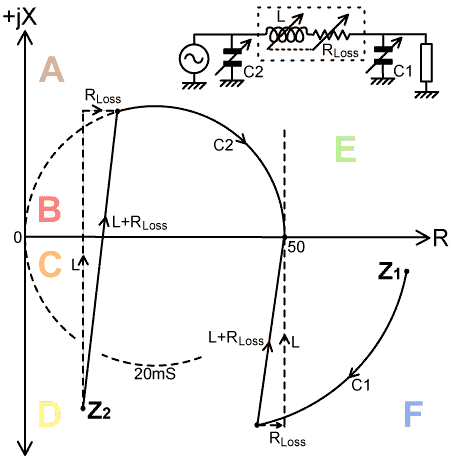
back to read jX for the inductance adjustment. If the load impedance lies in regions B, C, or D, L is first increased until G=20mS with jX positive. C2 is then increased until jX=0. In this case, adjustment of C1 is not required. The effect of coil losses: In the real world, of course, inductors have losses, and these will cause deviations from the idealised behaviour so far outlined. Recall that the effect of adding series resistance is to move the resultant impedance along a line of constant reactance. This means that the loss resistance of the coil (increasing as more turns are added) will cause the resultant impedance to come out a little higher than expected, as illustrated below: |
|
In the case of impedances lying in regions A, E,
and F, as represented by impedance Z1
in the diagram above, it will be necessary to increase C1 slightly to compensate for the losses in
the coil. In practice, C1 will initially
be used to bring the impedance on to the 50Ω, constant
resistance line; but the R=50 null reading will drift a little
high as L in increased, and C1 may need
to be retouched. A large readjustment of C1
indicates that the coil losses are high, a situation that is
sometimes unavoidable; but it may mean that the coil needs to
be redesigned, or that the AMU enclosure is suspect [11].
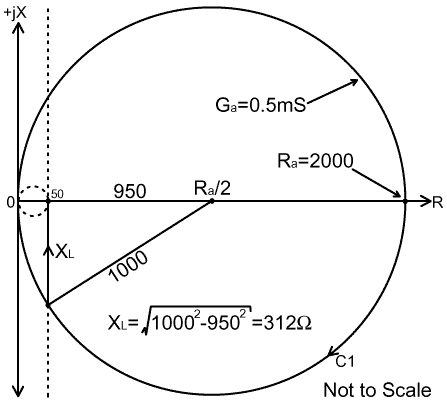
In the case of impedances lying in regions B, C, and D, as represented by impedance Z2 above, losses in the coil will cause the resultant impedance to hit the 20mS circle slightly to the right of the expected point, but since this is an intermediate step, it will not be noticeable to the operator. To put a figure on the actual loss resistances that may be encountered, recall that the RF resistance of a coil is related to its Q by the equation: Q=XL/RLoss. The Q of coils can vary widely, but a well designed AMU coil in a spacious enclosure might have an unloaded Q of about 200. An electrically short antenna (with an impedance in region D) might require about 1000Ω of inductive reactance to bring it on to the 20mS circle with jX positive. In this case, with a QL of 200, RLoss=XL/QL=5Ω. A near full-wave dipole with a λ/2 transmission line (with an impedance in region E or F) on the other hand, might have an input resistance of about 2000Ω. A little trigonometry (see the diagram below) will show that adjustment of C1 will shift this impedance on to the 50Ω constant resistance line at jX=-312Ω, i.e., it will require 312Ω of inductive reactance to complete the match, and with QL=200, RLoss will be about 1.6Ω. |
|
The diagram above illustrates the point that if an antenna has
an input resistance of Ra, the constant
conductance circle (Ga) on which Ra lies is centred on the point 0.5Ra+j0.
Simple application of Pythagoras' theorem will therefore give
the point at which the circle touches the 50Ω constant
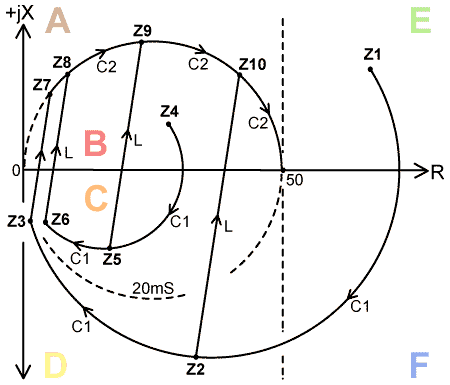
resistance line and hence the amount of inductive reactance XL needed to reach 50+j0 Ω. Capacitors incidentally, also have losses. These are small in comparison to coils, but may sometimes be significant. A typical air-variable capacitor with a wiping rotor-contact might have a Q of about 1000, and a vacuum-variable capacitor perhaps 5000. The series equivalent loss resistance is obtainable from the expression: Qc=-Xc/RLoss. It should perhaps be stressed here, that although losses will cause deviations in the matching process, such deviations are not likely to be significant in terms of SWR. The criteria for achieving 1.2:1 SWR are: R between 45 and 56Ω, G between 17.5 and 22.5mS, and Load phase angle φ ( =arctan(X/R) ) between -7 and +7° [9]. Thus, if components of reasonable quality are used, there will not be a significant mismatch even if the controls are not retouched to correct for the effects of losses. Note also that a typical SWR meter with a directionality of about 20dB cannot measure SWR of less than 1.22:1 (the reflected power reading may drop to zero, but this is due to detector diode non-linearity). Twin-detector nulling bridges however (as used in the Match Meter), can in principle, measure arbitrarily small matching errors. Matching with both capacitors: From the discussions above, we see that matching can be accomplished using either C1 or C2, and that adjustment of both capacitors is not necessary. A not unusual practice however, is to adjust the π-match 'in the dark' (monitoring only input SWR), using both capacitors, and it is interesting to see what happens when this is done. As we shall see, the π-match rightly has a reputation for being able to match anything; but we should be a little suspicious of the fact that this also includes open-circuits and dead-shorts, neither of which are renowned for their radiating abilities. Shown below are some of the Z-plane excursions that can be achieved by using both capacitors: |
|
We will begin by considering point Z1,
which is shown in region E, but could just as well be
in regions A or F. Z1
can be matched by increasing C1 to bring
the impedance a little inside the 50Ω line at point Z2, then increasing L to reach Z10, and then increasing C2
to reach 50+j0. In this case, the amount of inductance
required is a little larger than if C1
alone were used, i.e., maximum efficiency will not be achieved
[12], but no great harm is
done and the additional reactance will give improved harmonic
rejection. Injudicious adjustment of C1
however, may also bring the intermediate impedance to point Z3, which as we shall see shortly, is a
much less attractive proposition. In the case of Z4, which is shown in region B but could just as well be in region C, adjustment of C1 results in a somewhat pointless excursion to Z5, but again no great harm is done as long as the increase in C1 is not too great. Too much C1 however, and we arrive at point Z6. Points Z3 and Z6 are shown a little removed from the origin for clarity in the diagram, but they represent situations in which it makes little difference if the antenna is disconnected or shorted out. In effect, C1 has swamped the antenna impedance and the antenna has become irrelevant. If the antenna is removed, the point Z3 or Z6 will jump onto the R=0 axis at jX slightly negative; if the antenna is shorted, the point will jump to 0+j0; but the difference will hardly be noticeable in the absence of field strength or antenna current measurements. Obtaining 1:1 input SWR is perfectly possible however, because, due to losses, adjustment of L gives rise to a slanted or curved trajectory instead of a vertical line of constant resistance. This means that we can always get onto the 20mS constant conductance circle at positive jX even when starting from 0+j0. Points such as Z3 and Z6, close to or on the R=0 axis represent situations in which virtually all of the transmitter power is dissipated in the matching network inductor. Consequently, given enough power, and a big enough C1, the π-match can be sent up in flames. Note that if the maximum capacitance of C1 is not large enough to permit this situation at lower frequences, it will be large enough at higher frequencies. The foregoing hopefully illustrates the point that a π-match network should never be used without some kind of output indicator. Output level measurement moreover, will indicate maximum efficiency when the least possible amount of inductance is used consistent with keeping as far away as possible from the R=0 line. This means that the single capacitor matching strategy will give greatest efficiency, and the operator will be driven to increase either one capacitor or the other, but not both, if a proper set of adjustment diagnostics is used. Harmonic suppression goes out of the window if power throughput is the adjustment criterion, especially since some antenna impedances will require the controls to be set for minimum effect; in which case it is time to fit low-pass filters in the transmitter, and consider the merits of the L-network described below. |
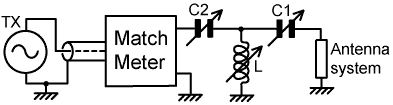
| 3. The L-match. |
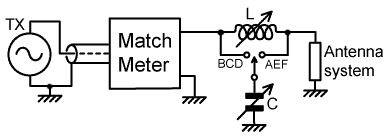
|
The L-match, of course, is just the same as the π-match but
with the single capacitor matching policy enforced. Consequently,
the applicable Z-plane diagrams are the same as those given earlier
for the π-match, and they will not be repeated here. As before,
L and C must be notionally removed for any initial Match Meter
analysis, and the switch in the diagram is labelled to indicate
the appropriate configuration for a given Z-plane region. Note
incidentally, that in most texts on the L-network, the switch
position here marked 'BCD' is marked 'Z<50Ω',
and the position here marked 'AEF' is marked 'Z>50Ω'.
The common designations therefore give an incorrect assignment
of impedances in region A (not that an operator using
an SWR bridge would know). It should be stressed here, that the L-match is not a cut-down or restricted range version of the π-match. It is simply a better circuit, which is more difficult to mis-adjust, does not suffer from the unwanted residual capacitance of an unused capacitor, and is cheaper to build. As with all ATUs however, the residual inductance and capacitance at minimum settings must be as low as possible if matching is to be accomplished over a wide frequency range. Consequently, if standard air-variable capacitors are used (sometimes having little better than 10:1 capacitance range), it may prove necessary to gang several capacitors together, and disconnect gangs as the operating frequency is increased. The preferable alternative is to use a vacuum variable capacitor (typically 100:1 range). |
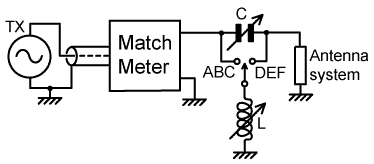
| 4. Switched-inductor π-match: |
|
This matching network saves on the expense of a variable inductor,
but it suffers from the same design problem as roller-inductors,
which is that of whether or not to short out the unused turns.
If the coil is wound as a single solenoid, with mutual inductance
between the turns, shorting out the unused turns will result
in reduced Q due to eddy currents. If the unused turns are not
shorted however, and only a small part of the coil is in use;
very high voltages can be developed at the open-circuit end and
corona and arcing may result. One solution to this problem is
to short the unused turns when the overwind is large, but leave
them open when the overwind is small. Another solution is to
make the inductor out of a string of separate coils in series,
with minimal mutual inductance (i.e., coils in proximity mounted
at right-angles to each other), in which case unused sections
can be shorted-out with impunity, but it will take a much greater
length of wire to to achieve a given inductance. Consequently,
the design of efficient tapped inductor networks to cover the
entire HF spectrum is more difficult than first meets the eye,
and good solutions tend to comprise groups of isolated tapped
inductors in series. The matching process using a switched-inductor π-network is illustrated in the Z-plane diagram below: |
|
If the load impedance lies in regions A, E, or
F, C1 is first increased to bring
the resultant impedance to the point Z1
on the 50Ω constant resistance line. L is then switched
into circuit and a tap selected so that jX is just positive,
as represented by point Z2. A small
increase of C1 then brings us to the 20mS
constant-conductance circle at point Z3,
and adjustment of C2 moves the impedance
to 50+j0 to finalise the match. Note however, that there
may be two discernable nulls in the conductance reading (at Z3 and Z4)
on going from point Z2 towards
the 20mS circle. This effect depends on the extent to which the
arc Z2-Z3-Z4 overlaps the 20mS circle (Z3
and Z4 converge when the circles
just graze) but if it is apparent, the null involving the least
amount of C1 is the best choice. Note
also, that if the inductance steps are too coarse the arc Z2-Z3-Z4 may never touch the 20mS circle, and
a perfect match will not be possible. The arc Z2-Z3-Z4 incidentally,
is just the constant conductance circle of C1
in parallel with the load as seen through the inductor,
i.e., the circle is moved upwards by an amount equal to XL, and slightly to the right by an amount equal
to the coil loss resistance. If the load impedance lies in regions B, C, or D, inductance is first added until the impedance is just inside the 20mS circle (G>20mS) with jX positive, i.e., the switch is advanced until G is just less than 20mS with jX positive, and then clicked back one notch. C1 then brings the conductance to 20mS at Z6, and C2 completes the match. |
|
5. Tapped inductor with interpolation capacitor: Instead of configuring the switched-inductor matching unit as a π-network, it can also be configured as a continuously variable L-network by wiring one of the capacitors so that it can be used to interpolate between the coil taps. |
| In this case, if slightly more than the required amount of inductance is selected, a small amount of capacitive reactance in series with the coil can be used to back-off the inductance as far as the preceding tap. The result is a continuously variable inductance. The interpolation capacitor needs to have a low reactance at the frequency of operation when fully enmeshed, and it must be possible to reduce the capacitance to a point where its reactance is equal to the largest inductive reactance step that will be encountered. This configuration is often used in professional HF radio systems, but finds surprisingly little favour among radio amateurs [10]. The interpolation element might also be a small variable inductor, such as a variometer, but variable capacitors are cheaper and easier to acquire. |
|
6. The T-match: Weak signal overheard on 80m: "I've come to the conclusion with this T-match, that all you do is set the capacitors about half-way, and it doesn't really matter what you do with the coil". |
| The T-match is a widely used network, favoured because it can match a given range of load impedances using smaller values of capacitance than are required for a π or L network. Detailed modelling of the circuit however shows that the price paid for using smaller components is a reduction in efficiency; and best performance is achieved when the capacitors are made as large as possible (consistent with the minimum capacitance not being excessive at higher frequencies). The Z-plane manipulations performed by this network are shown below. It is assumed in this case that the capacitors are initially set to maximum capacitance, and the coil to maximum inductance. |
|
In the case of load impedances falling in regions A, B,
and C, C1 is first adjusted until
the conductance is 20mS with jX negative (point Z1). L is then reduced until the impedance
reaches 50+j0, thereby completing the matching operation.
Note however, that losses in the coil will cause the impedance
to spiral inwards slightly, and it may be necessary to re-touch
C1 to achieve exactly 1:1 SWR. There is
no need to adjust C2 however, and the
influence of C2 is minimised by making
it as large as possible. If the impedance lies in regions D, E, or F, L is first reduced until R=50 with jX positive (point Z2). C2 is then reduced until the impedance reaches 50+j0. Note in this case that losses in the coil will cause the impedance to spiral inwards slightly during the L-adjustment step, causing the impedance to arrive at the 50Ω constant resistance line a little early, but since this is an intermediate step, the effect will not be noticeable to the operator. In this case, there is no need to adjust C1, and the influence of C1 is minimised by making it as large as possible. Most commentators on the T-match instruct the user to start by setting both capacitors about half-way (see, e.g., [14] ). It is, of course, possible to construct a Z-plane diagram showing what happens when both capacitors are used, but since the T-match is effectively a high-pass network, even less good will come of it than in the π-network case. In the case of impedances ZD and ZF in particular, reduction of C1 can only move the impedance further into the -jX region, requiring it to describe a larger circle of constant conductance (lower parallel XL) on its way around to the R=50 line in the +jX zone. This means more losses in the coil, as might also be expected when it is observed that reducing C1 has the effect of progressively disconnecting the antenna. If the coil is lossy enough, it may be possible to disconnect the antenna completely, keep reducing the inductance until the coil loss resistance reaches 50Ω, then reduce C2 to match all of the transmitter power into the coil losses. In order to gain a qualitative understanding of the losses associated with an inductance placed in parallel with an impedance (i.e., the losses in all of the T-derived networks); it is important to understand that the losses increase as parallel inductance is reduced. In the π-match (series inductance) case, we observed that the losses in the system (neglecting capacitor and inter-wiring losses) increase as the inductance is increased, this being due primarily to the increase in wire length. In the parallel case however, we need to think in terms a a reciprocal measure of loss resistance, i.e., Q=XL/RLoss. If a wire is wound into a solenoid, the loss resistance of the wire is proportional to the length of wire used and therefore proportional to the number of turns, n. Due to the effect of mutual inductance however (i.e., the magnetic coupling between adjacent turns) the inductance is roughly proportional to N², i.e., inductance increases faster than loss resistance as the number of turns is increased. This means that Q increases with N, and in parallel cases we should always try to effect a match with the largest possible value of inductance. The unloaded Q of a good roller inductor may be in the 100 to 150 region when the number of turns used is large, but may be only in the 20 to 50 region when only a few turns are used (such as is the case when working on the 10m band). |
|
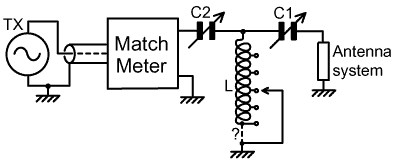
7. Reciprocal L-network: Having observed, yet again, that one of the variable capacitors in a popular matching network is, in principle, redundant; we will consider the network shown below. Note that this configuration is sometimes called an L-match, but here we will call it the reciprocal-L match to distinguish it from the L-network described earlier. Once again, there is no need to draw a Z-plane diagram because it is the same as for the T-match; except that unwanted impedance shifts and inefficiency due to the residual reactance of the unused capacitor are eliminated. |
| The disadvantage of the reciprocal L network is that, for a given matching range, it requires larger maximum values of L and C than for a T-match. There is however an alternative reciprocal L circuit, which can be implemented as a modification to an existing T-match tuner (with no need to alter the markings on the front panel), and which can revert to the T-configuration if a given load proves to be unmatchable using an L-configuration [15][16]. |
|
High-voltage variable air-capacitors often undergo 360° rotation
even though only 180° is used. If that is the case, a cam
can be mounted on the capacitor shaft and arranged to operate
a shorting switch during the unused half of the rotation. The
ability to revert to a T-network caters for situations in which
there is insufficient capacitance to effect a match without using
an intermediate transformation (i.e, when both capacitors are
needed). The old trick of turning over the corner on one of the
rotor plates, incidentally, is not recommended; since it may
not make a particularly good contact, and the scarring of the
plates that occurs will reduce the capacitor breakdown voltage.
A separate article describes the fitting of capacitor shorting
switches to the MFJ989C Versatuner. In addition to increasing efficiency, the reciprocal-L network eliminates one further problem of the T-match, which is that the voltage across the inductor is controlled neither by the transmitter nor by the load. This means that if the loaded Q of the coil becomes excessive, which it can if both capacitors are used, very large voltages can be developed. Large voltages may, in any case, be developed if the load is highly reactive, but the T-network exacerbates the problem. |
|
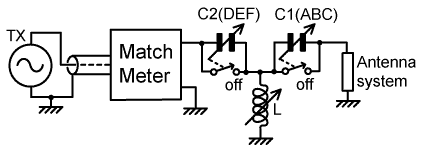
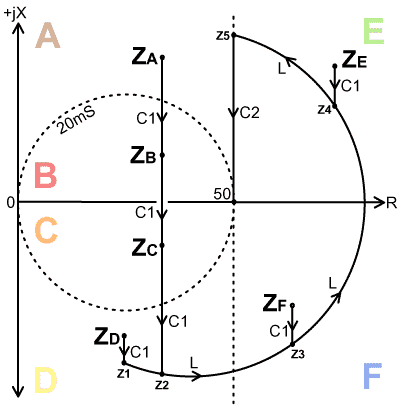
8. Switched inductor T-match: This is another popular matching network that saves on the expense of a variable inductor. |
| The operation of this network depends on the fact that C1 can be used to adjust the diameter of the constant conductance circle around which the intermediate impedance is moved by the inductor. Adjusting the diameter of the circle adjusts the length of the arc described; the object of the exercise being to select an arc length that brings the impedance to the 50Ω constant resistance line and corresponds exactly to one of the available inductance settings |
|
In the case of load impedances in regions A, B,
and C, C1 is first reduced until
the conductance is just less than 20mS with jX negative
(point Z2). L is then reduced stepwise
until the resistance is just less than 50Ω with jX
positive (i.e., the impedance is moved into region A).
A further small reduction of C1 will then
expand the arc Z2-Z5
until Z5 lies exactly on the 50Ω
constant resistance line, at which point C2
can be adjusted to complete the match. In the case of a load impedances in regions D, E, and F, L is reduced first until the resultant impedance is just inside region A. C1 is then reduced slightly to expand the arc produced by L until Z5 lies exactly on the 50Ω constant resistance line; at which point C2 is adjusted to complete the match. The advantage of the switched-inductor T-match (compared to the switched-inductor π-match), is that C1 or C2 (depending on the Z-plane region) provides an effective interpolation between coil taps, i.e., a perfect match can still be achieved if the tappings are somewhat coarse [17]. Fine taps however minimise unnecessary excursions of the capacitors and help to maintain efficiency. |
|
9. The Differential-T match: ("Differential-T" is a trademark of MFJ Corp.) |
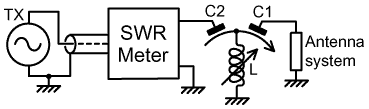
| The differential-T match has capacitors C1 and C2 ganged in such a way that when one is at minimum capacitance, the other is at maximum capacitance. This enables a wide range of impedances to be matched with only two controls, and gives only one possible matching solution for each impedance encountered [18], [19]. The differential-T match is not amenable to the Match Meter approach because the matching elements cannot be adjusted independently, and so should be adjusted with the aid of an SWR meter. At high frequencies, where one capacitor will be almost at minimum and the other almost at maximum, the efficiency will be almost the same as as that of a T-match using the same component values, because the capacitor close to its maximum setting will have very low reactance. At lower frequencies however, a two-capacitor matching policy is enforced, and the efficiency will generally be somewhat lower than that achieved with a T-match with one of the capacitors fully enmeshed or shorted. It is therefore not a configuration for efficiency purists, but is nevertheless a good solution to the ambiguity problem, and therefore a good tuner for recommendation to beginners. A Z-plane diagram for the differential T-match in the low-frequency regime is shown below: |
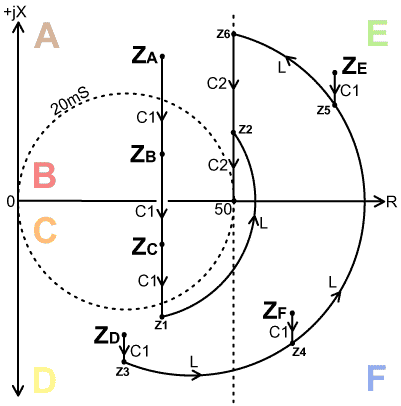
| From the diagram, it should be apparent that the relative amounts of C1 and C2 required are dictated by the need to hit the 50Ω constant resistance line with jX positive (Z2 and Z6). Note that in the low frequency regime, where C2 always has some significant reactance, the arc Z1-Z2 can never quite lie on the 20mS constant conductance circle; and therefore the parallel inductance will always be slightly lower than in the normal T-match case, and the losses slightly higher. |
|
10. The "Ultimate" Transmatch? The "Ultimate" transmatch circuit was devised by Lew McCoy, W1ICP, and first appeared in the ARRL journal 'QST' in 1970 [20]. It is a T-network with an additional shunt capacitor placed across the transmitter terminals and ganged to the transmitter-side capacitor in such a way that the two capacitors increase simultaneously. |
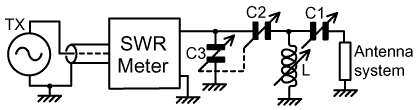
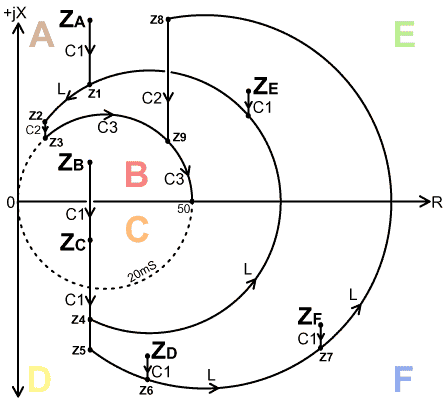
| The circuit was intended to give improved harmonic attenuation compared to that offered by a normal T-network, and does so in a limited way that depends on the load impedance. It came under fire in the early 1980s however, as a result of efficiency calculations carried out by Walt Maxwell, W2DU. The problem can be seen clearly by drawing the Z-plane diagram: |
|
Impedance matching strategies for various loads are shown in
the diagram above, but the first point to note is that the intermediate
impedance can never be manipulated onto the 50Ω constant
resistance line. Moving around circles of constant conductance
close to the 20mS circle always forces the intermediate impedance
close to the jX=0 axis (point Z2),
whereas atempts to avoid this condition by reducing C3
also reduce C2 and result in giant circles
(arc Z5-Z8).
Thus large values of C2 and C3
enforce a small vertical movement and a large circular movement,
and vice versa. In either case, the parallel inductance required
to effect a match is always much lower than in the conventional
T-match case, and the inductor Q suffers as a result. An interesting point worth noting here is that inefficient modified T-networks such as the 'Ultimate' are often defended on the basis that they can match a wider range of impedances than a normal T-match for a given inductor size. This however is true of any parallel inductor network that prevents minimisation of the radius of the circle of constant conductance on which the intermediate impedance moves; because larger circles of constant conductance mean lower inductance values for a given impedance transformation. T-derived networks are very forgiving in this respect, allowing the trading of efficiency against cost; but in determining matching networks for HF radio transmitters, a large inductance is best. An inauspicious fate awaits anything that presumes to call itself 'The Ultimate'; although to be fair, it was probably so called because of its enormous matching range in comparison to the then-prevalent networks intended for use with co-ax fed antennas. The Ultimate transmatch must now be regarded as an obsolete circuit; but to those who still own and use such units, it should be obvious where to put the wire cutters. With the offending C3 removed from circuit, it should still be possible to match any impedance with occasional recourse to a dual-capacitor matching strategy; and by connecting the spare C3 across C2 it should be possible to increase the efficiency still further, provided that the minimum capacitance does not become too large for matching high-impedance (high |Z|) loads at high frequencies. |
|
11. The SPC Transmatch: The Series-Parallel Capacitor transmatch was devised by Doug DeMaw, W1FB, in 1980, in an attempt to obtain better harmonic suppression than that offered by the 'Ultimate' transmatch [21]-[25]. The harmonic measurements on which the design was based however, were made using resistive loads, and have attracted criticism regarding their applicability to real antenna systems. In this case, the Spurious Parallel Capacitor is placed across the coil and ganged to the antenna-side capacitor in such a way that the two capacitors increase in value simultaneously. |
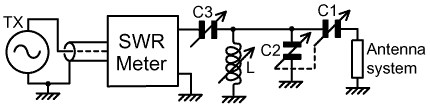
| From an impedance matching point of view (which we might be inclined to adopt when considering matching networks), the effect of C2 is to cancel the effect of the inductor L to a greater or lesser extent depending on the load impedance. Example impedance matching operations are shown below: |
|
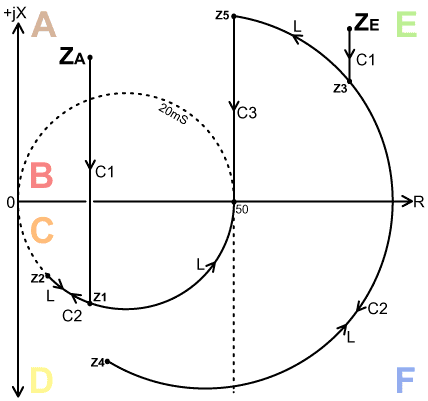
In the case of impedance ZA, assuming
that C3 can be made large so that its
influence can be neglected, the SPC transmarch forces the route:
ZA→Z1→Z2→50+j0. If ZA
is moved downwards towards zones B or C, C1 must be increased, thereby increasing C2 and forcing point Z2
closer to 0+j0. In the case of impedance ZE, the SPC transmarch forces the route: ZE→Z3→Z4→Z5→50+j0. Recall that in the T-match, C1 is best set at maximum for regions D,E, and F, but in this case reduction of C1 helps to reduce the vastness of the excursion due to C2. In either case, the effect of C2 is to force a reduction in the value of L in order to compensate for its presence. This, of course, results in lower efficiency than would prevail in the case of a T-match using the same coil, but means that the SPC circuit will have the wider matching range. The only situation in which the efficiency of the SPC transmatch will approach that of the T-match is in a low-frequency regime involving a highly inductive load impedance. In that case, the required value of C1 will be small, and so the influence of C2 will also be small; and the harmonic attenuation will be little better than that given by a T-match. The SPC transmatch remained the ARRL standard for many years after its introduction in 1981. The design was dropped by the 19th edition of the ARRL Antenna Book (2000) however, as a result of efficiency calculations. The standard wisdom is now that properly designed transceivers and linear amplifiers should already meet legal requirements; and any additional harmonic attenuation required should be effected by means of low-pass filters inserted in the constant-impedance signal-chain between the transmitter and the matching network. For those who still own and operate SPC tuners; it should once again be obvious where to put the wire cutters, and that the redundant C2 may be placed in parallel with C1 provided that the minimum capacitance does not preclude the matching of inductive loads at high frequencies. Note incidentally, that it is not the presence of a capacitor in parallel with the coil to which we object, but the fact that the capacitor is ganged to C1. Every coil has a parallel self-capacitance, and there will be additional capacitance due to the wiring and nearby metalwork. The effect of this at low frequencies is to increase the apparent inductance. As the frequency is increased, a point will be reached at which parallel resonance occurs; in which case the apparent inductance becomes infinite, and the coil is effectively disconnected except for the dynamic resistance of the L//C network (which can be quite large as long as the L/C ratio is large. See [AC Theory, Section 16] ). Hence, parasitic parallel capacitance increases the effective inductance variation range, and allows infinite maximum inductance at frequencies above the point at which self-resonance occurs when the inductor is at its maximum setting. A small capacitance in parallel with the coil is neither avoidable, nor particularly undesirable. |
|
12. Discussion: The theoretical treatment of antenna tuners can be undertaken in much greater depth than has been attempted so far; but what we have developed, hopefully, is a qualitative way of explaining how they work. A correct qualitative understanding should be sufficient to allow radio operators to make critical judgements regarding efficiency and network selection; and will indicate, to the more mathematically inclined, how to construct the appropriate circuit models. Harmonic attenuation calculations based on the idea that antennas are resistors are unacceptable; because it can be shown quite easily that, unless the antenna system can be specified rigidly, the harmonic attenuation available from antenna tuners is just a matter of luck. These findings obviously have implications with regard to equipment design, selection, and operating practice, and may be summarised as follows: Some discussion of matching network efficiency, particularly in relation to the various basic and modified T-networks, is given in refs: [16] and [26]-[28]. |
© D W Knight 2007 - 2009.
David Knight asserts the right to be recognised as the author of this work.
|
|
|
|
|
|